What Is the Fisher Effect?
 The Fisher Effect is an economic theory that describes the relationship between nominal interest rates, inflation expectations and real interest rates.
The Fisher Effect is an economic theory that describes the relationship between nominal interest rates, inflation expectations and real interest rates.
It is an economic theory introduced by economist Irving Fisher in the 1930s. It consistently describes the relationship between inflation and both real and nominal interest rates. According to the Fisher Effect, the real interest rate is equal to the nominal interest rate minus the expected rate of inflation. In this equation, all rates used should be compounded. The result, in practice, is that as inflation rates go up, real interest rates go down, when nominal rates don’t increase at rates equal to those of inflation.
This effect is not always immediately visible, but over time, it is a consistent economic pattern. The Fisher effect formula not only plays an important role in economics and business. Also, it has applications that can benefit individuals and investors.
The Fisher Effect Formula
The formula used to calculate the Fisher Effect requires three important data parameters. These are the nominal rate of interest, the real rate of interest, and the inflation rate that is currently expected.
(1 + i) = (1 + r) x (1 + e)
- i = Nominal Interest Rate
- r = Real Interest Rate
- e = Expected Inflation Rate
The Fisher Effect – A Deeper Look
Fisher’s equation reflects that the real interest rate can be taken by subtracting the expected inflation rate from the nominal interest rate.
The Fisher Effect demonstrates that the money supply influences the inflation rate and nominal interest rates together. For instance, when monetary policy shifts to increase the inflation rate by 5 percent, the result is that the nominal interest rate also increases by that same percentage. Alterations in the money supply do not directly alter the real interest rate. However, changes in the nominal interest rate are associated with alterations in the money supply.
The Fisher Effect can be seen each time you go to the bank. The interest rate listed on a savings account is effectively the nominal interest rate. For example, say the nominal interest rate on a savings account is 3% and the expected rate of inflation is 2%. In effect, the money in the savings account is really growing at 1%. The smaller the real interest rate, the longer it will take for savings deposits to grow. At least, when observed from a purchasing power perspective.
Nominal Interest Rates and Real Interest Rates
- Nominal interest rates reflect the financial return an individual gets when he deposits money. For example, a nominal interest rate of 4% per year means that an individual will receive an additional 4% of his deposited money in the bank.
- Real interest rates consider purchasing power in the equation as it grows or declines over time.
In the Fisher Effect, the nominal interest rate is the provided actual interest rate that reflects the monetary growth over time. The real interest rate is the amount that mirrors the purchasing power of the borrowed money as it grows or declines over time.
The Fisher Effect Example
The Fisher effect has short-term practical applications you can use in everyday life. It is an estimate of purchasing power according to rates of inflation. Therefore, you can use it to define the “real” rate of return on an investment. At least, in terms of what your profits will buy.
For example, if you purchase a 12-month certificate of deposit for $5,000 at an interest rate of 0.94 percent and inflation remains constant, you will have $5,047.22 at the end of the year. If inflation rises 2 percent over the course of the year, however, you actually lose money on the investment, as your profits and the purchasing power of your money decrease by $53.50 or 1.06 percent, leaving you with only $4,993.72 to spend: 2.0 – .94 = 1.06 5047.22 * 1.06 = 53.50 5047.22 – 53.50 = 4993.72 (Source: zacks.com)
Importance in Money Supply
The Fisher Effect is more than just an academicequation. It shows how the money supply affects the nominal interest rate and inflation rate together. For example, consider a change in a central bank’s monetary policy. Say it pushes the country’s inflation rate to rise by 5 percentage points. As a result, the nominal interest rate of the same economy would follow suit. It would increase by 5 percentage points as well. It may be assumed that a change in the money supply will not affect the real interest rate. However, it will directly reflect changes in the nominal interest rate.
Monetary Policy
The central bank in an economy is often tasked with keeping inflation in a tight range. The practice is to prevent the economy from overheating and inflation spiraling upwards in times of expansion. However, it is also important to have a small amount of inflation to prevent a deflation spiral. Deflation can push an economy into a depression in times of recession. The main tool available to most central banks is their ability to set the nominal interest rate. They achieve this through interventions like open market operations, changing reserve ratios, etc.
Given a fixed interest rate, an increase in the nominal interest rate will bring down inflation expectations and prevent overheating. Similarly, a decrease in the nominal interest rate can increase inflation expectations. The result is to spur more investment, thereby avoiding a deflation spiral.
The International Fisher Effect (IFE)
The International Fisher Effect (IFE) is an economic theory. It states that the expected disparity between the exchange rate of two currencies is approximately equal to the difference between their countries’ nominal interest rates. The IFE is an exchange-rate model that extends the standard Fisher Effect. It is often used in forex trading and analysis. The IFE is based on present and future risk-free nominal interest rates rather than pure inflation. It is used to predict and understand the present and future spot currency price movements. It is assumed that the risk-free aspects of capital must be allowed to free float between nations that comprise a particular currency pair. However, this may not be the actual case depending on the currencies and countries involved.
Bottom Line
Knowing the real rate of interest is essential for making good investment decisions. Using the Fisher effect in calculating short-term effects can prove both useful and enlightening. The results become more reliable and significant when applying it in the long term. Compound calculations should be made using your time frame for investing, initial investment amount, nominal interest rate and varying rates of inflation. The effect can be a useful tool for analyzing the potential of an investment. It can also help determine at what point in an economic cycle it makes sense to sell.
Up Next: What Is a Gravestone Doji?
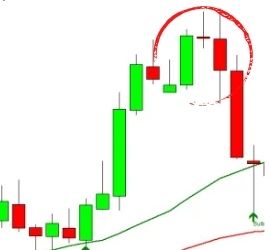
License (CC BY-SA 4.0)
A Gravestone Doji is a bearish reversal candlestick pattern on a stock price trading chart. It is formed when the open, low, and closing prices are all near each other with a long upper shadow. The candlestick appears like an upside-down “T”. The long upper shadow suggests that the bullish advance at the beginning of the session was overcome by bears by the end of the session. This scenario often comes just before a longer-term bearish downtrend.
The interpretation is that the bulls attempt to push to new highs over the session. However, the bears push the price action to near the open by the session close. So the long upper shadow can be interpreted that the bulls are losing momentum. Conversely, the bears are gaining momentum.
The Gravestone Doji can also be found at the end of a downtrend. However, it is more common to find one at the end of an uptrend. The Gravestone Doji suffers from the same reliability issues found in stock pricing chart visual patterns. As a precaution, traders should not act on a Gravestone Doji unless the next candle provides confirmation that a reversal is actually taking place.




